Cấp số nhân là một khái niệm hấp dẫn trong toán học và có sử dụng rộng rãi trong nhiều lĩnh vực. Công thức tính tổng của cấp số nhân có lợi cho cả các bài toán lý thuyết và thực tế. Với mục đích cung cấp kiến thức chuyên sâu hơn về cấp số nhân, bài viết này sẽ xem xét chi tiết công thức này, từ khái niệm cơ bản đến các ứng dụng thực tế.
1. Giới thiệu về cấp số nhân
Điều gì được gọi là cấp số nhân?
- Cấp số nhân là một dãy số mà mỗi số hạng sau bằng số hạng trước nhân với một hằng số. Tỷ lệ chung là một hằng số được sử dụng để mô tả cấp số nhân. Công thức [a_n = a_1 \cdot r^{(n-1)}] có thể được sử dụng để hiển thị mỗi số hạng trong cấp số nhân.
- Trong đó, số hạng thứ n (a_n), số hạng đầu tiên (r), tỷ lệ chung (n) và chỉ số số hạng có đặc điểm của cấp số nhân.
Cấp số nhân có một số đặc điểm, chẳng hạn như
- Tăng trưởng nhanh: Dãy số sẽ tăng nhanh nếu tỷ lệ chung (r > 1).
- Giảm xuống: Dãy số sẽ giảm xuống nhưng vẫn dương nếu bắt đầu từ số dương nếu (r < 1).
- Hình ảnh đồ thị: Hình dạng cong của đồ thị cấp số nhân thường cho thấy sự tăng trưởng hoặc giảm theo cấp số.
Lịch sử và sự phát triển
- Cấp số nhân đã được nghiên cứu trong một thời gian dài trong toán học. Các nhà toán học như Euclid và Archimedes đã khám phá và ghi nhận nhiều đặc điểm của dãy số này. Ngày nay, công thức tính tổng của cấp số nhân là một phần chính của giáo dục toán học ở nhiều quốc gia.
2.Tổng quát về cấp số nhân
Cấp số nhân có thể được tìm thấy trong nhiều lĩnh vực khác nhau, chẳng hạn như tài chính, vật lý, sinh học, v.v.
Các loại cấp số nhân khác nhau
- Cấp số nhân chính có hai loại:
- Cấp số nhân hữu hạn là một dãy số có số hạng cuối cùng. Chẳng hạn: (2, 6, 18, 54).
- Cấp số nhân vô hạn được định nghĩa là một dãy số không có số hạng cuối cùng. Ví dụ: (1, 2, 4, 8) )
Tầm quan trọng của tỷ lệ chung
- Tính chất của cấp số nhân phụ thuộc vào tỷ lệ chung. Nó có tác động đáng kể đến sự gia tăng hoặc giảm sút của dãy số. Hiểu rõ tỷ lệ chung giúp dự đoán hành vi của cấp số nhân.
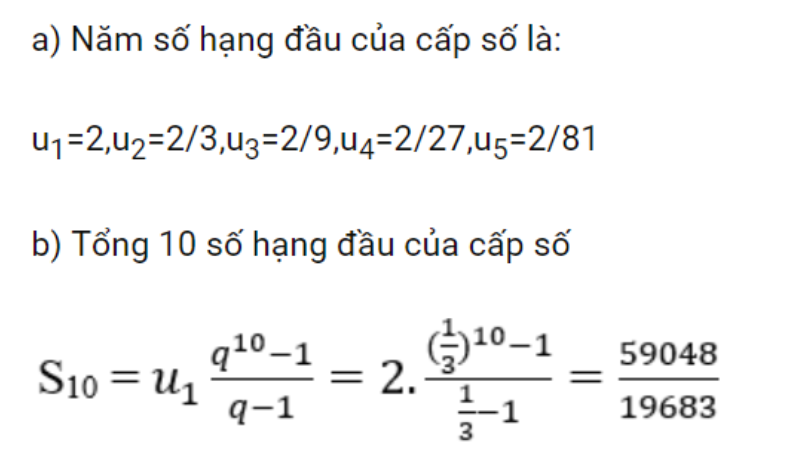
3. Công thức tính tổng của cấp số nhân hữu hạn
Công thức đơn giản để tính tổng cấp số nhân hữu hạn rất hữu ích. Sau đây là biểu diễn của công thức này:
- [S_n = a_1 frac{(1 – r^n)}{(1 – r)} và (r không bằng 1)]
- Trong đó, S_n là tổng số hạng đầu tiên n, a_1 là số hạng đầu tiên, r là tỷ lệ chung, và n là tổng số hạng đầu tiên.
Tìm hiểu công thức
- Có hai phần chính của công thức trên:
- Vai trò của số hạng đầu tiên trong dãy số được thể hiện bởi phần tử (a_1). Điều này chứng minh rằng giá trị ban đầu đóng một vai trò quan trọng trong việc xác định tổng của dãy số.
- Phần tử (frac{(1 – r^n)}{(1 – r)} cho thấy mối quan hệ giữa tỷ lệ chung và số lượng hạng. Mỗi khi có một tỷ lệ chung lớn hơn 1, tổng sẽ tăng theo cấp số nhân.
Một ví dụ cho thấy
- Ví dụ cụ thể về tính tổng của cấp số nhân sẽ giúp bạn hiểu rõ hơn: Giả sử chúng ta có cấp số nhân 2, 6, 18, 54 và (r = 3).
- Tính toán tổng thể (S_4): [S_4 = 2 phần trăm (1 – 3^4) và (1 – 3)} = 2 phần trăm (1 – 81) và (2 phần trăm) = 80 ]
- Theo kết quả, tổng của bốn số hạng đầu tiên là tám mươi.
4. Ứng dụng của công thức tính tổng của cấp số nhân
Công thức tính tổng của cấp số nhân hữu hạn là một lý thuyết toán học tuyệt vời với nhiều ứng dụng thực tế.
Tài chính
- Để tính lãi suất kép, bạn có thể sử dụng công thức này. Tình huống cấp số nhân xảy ra khi bạn gửi tiền vào ngân hàng và nhận lãi suất hàng tháng.
Khi nói đến khoa học tự nhiên,
- Quy luật cấp số nhân áp dụng cho một số hiện tượng tự nhiên, chẳng hạn như sự phát triển của vi khuẩn hoặc sự lan truyền của virus. Chúng ta có thể dự đoán số lượng cá thể trong tương lai bằng cách sử dụng công thức tính tổng.
Trong lĩnh vực công nghệ,
- Thuật toán tìm kiếm và sắp xếp có thể hiển thị cấp số nhân trong lĩnh vực công nghệ thông tin. Hiệu suất và tốc độ xử lý dữ liệu có thể được cải thiện bằng cách tối ưu hóa các thuật toán này.

5. Ví dụ minh họa về tính tổng cấp số nhân
Xem xét một ví dụ khác để hiểu rõ hơn về cách sử dụng công thức tính tổng cấp số nhân: Giả sử một người đầu tư 1000 đồng vào một quỹ đầu tư có tỷ lệ tăng trưởng 10% mỗi năm. Mục tiêu của họ là sau năm năm, tính tổng số tiền họ nhận được.
Giải thích dãy số
Dãy số sẽ như sau:
- Năm một: Một nghìn * 1,1 = một nghìn một.
- Năm thứ hai, 1100 * 1.1 = 1210.
- Năm thứ ba: 1210 * 1.1 = 1331
- Vào năm 4, 1331 x 1.1 tương đương với 1464.1, và vào năm 5, 1464.1 x 1.1 tương đương với 1610.51.
- Tính toán tổng thể cho thấy S_5 bằng 1000 phần trăm.(1 – 1,1 5)(1 – 1.1) = 1000 frac(1 – 1.61051) -0.1 = 6105.1
- Tổng số tiền đạt khoảng 6105.1 đồng sau 5 năm.
Sự thay đổi trong suốt thời gian
- Sự phát triển theo cấp số nhân theo thời gian được thể hiện rõ ràng trong ví dụ này. Chính điều này đã chứng minh sức mạnh thực tế của việc sử dụng công thức tính tổng cấp số nhân.
6. Ý nghĩa trong toán học của công thức tổng cấp số nhân
Công thức tính tổng của cấp số nhân không chỉ quan trọng đối với việc giải quyết bài toán mà còn có thể được sử dụng trong nhiều lĩnh vực khác của toán học.
- Chức năng phát triển lý thuyết: Lý thuyết dãy số không thể thiếu công thức này, vì nó giúp chúng ta hiểu rõ hơn về các mối quan hệ giữa các hạng trong dãy.
- Liên hệ với các ngành khác nhau: Thật vậy, công thức tính tổng cấp số nhân có liên quan đến nhiều ngành khác nhau, chẳng hạn như thống kê, phân tích dữ liệu và cả khoa học xã hội.
7. Cách áp dụng công thức vào thực tế
Làm thế nào chúng ta có thể áp dụng công thức tính tổng của cấp số nhân vào thế giới thực?
- Tài chính của một cá nhân: Công thức này được sử dụng rộng rãi để lập kế hoạch tài chính, đặc biệt là để tiết kiệm và đầu tư.
- Công việc: Để dự đoán lợi nhuận và doanh thu trong tương lai, các công ty có thể sử dụng công thức tính tổng để lập kế hoạch phát triển hợp lý.
- Đào tạo: Trong giáo dục toán học, công thức này được sử dụng để giúp học sinh hiểu rõ hơn về các khái niệm số học.

8. Các câu hỏi thường gặp về công thức tính tổng của cấp số nhân?
Các câu hỏi phổ biến sau đây liên quan đến công thức tính tổng của cấp số nhân:
Làm thế nào một dãy có thể được coi là cấp số nhân?
- Để xác định một dãy là cấp số nhân, bạn phải xác định xem tỷ số giữa hai số hạng liên tiếp có không đổi hay không. Dãy số được coi là cấp số nhân khi tỷ số này là hằng số.
Khi nào thì công thức tính tổng cấp số nhân được sử dụng?
- Khi cần tính tổng số hạng của một dãy số mà mỗi số hạng sau bằng số hạng trước nhân với một công bội không đổi, bạn có thể sử dụng công thức tổng cấp số nhân. Trong các bài toán tài chính, kinh tế và kỹ thuật, công thức này đặc biệt hữu ích.
Trong đời sống, công thức tổng cấp số nhân có thể được sử dụng để làm gì?
- Tài chính: Công thức tổng cấp số nhân được sử dụng để tính lãi suất kép, giá trị tương lai của các khoản đầu tư hoặc các khoản vay lãi.
- Kinh tế học: Cấp số nhân thường là cơ sở cho mô hình tăng trưởng kinh tế, còn được gọi là dự đoán tăng trưởng theo thời gian.
- Vật lý: Khi nói đến phép tính liên quan đến sự phân rã hoặc tăng trưởng theo thời gian, chẳng hạn như phân rã phóng xạ hoặc tốc độ phát triển của tế bào, thì cấp số nhân cũng được sử dụng.
9. Kết quả
Chúng tôi đã đi sâu vào công thức tính tổng của cấp số nhân trong bài viết này. Mọi khía cạnh đã được mô tả chi tiết, từ khái niệm đến công thức và ứng dụng thực tế. Tôi hy vọng rằng bạn sẽ hiểu rõ hơn về cấp số nhân và có thể áp dụng chúng trong cuộc sống hàng ngày. Bạn cũng nên trao đồi cho mình kiến thức về bệnh thuỷ đậu để đề phòng, vì bệnh này rất dễ lây lan. Trên đây là công thức tính tổng của cấp số nhân , chi tiết xin truy cập website: congthuccapsonhan.com xin cảm ơn!
