Công thức cấp số nhân cấp số cộng là một trong những công cụ toán học phổ biến nhất và quan trọng nhất, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học cũng như trong cuộc sống. Hiểu và nắm vững công thức này sẽ giúp học sinh giải quyết các bài toán nhanh chóng và hiệu quả.
1. Công thức cấp số nhân cấp số cộng
Công thức cấp số nhân cấp số cộng là chuỗi số cấp số nhân và cấp số cộng có công thức riêng. Chúng ta sẽ xem xét định nghĩa, công thức và các đặc điểm cơ bản của hai khái niệm này để hiểu rõ hơn về chúng.
Cấp số cộng
Một dãy số được gọi là công bội (còn được gọi là d) trong đó mỗi số tiếp theo bằng số trước đó cộng thêm một số hằng định được gọi là công bội. Sau đây là công thức tổng quát cho cấp số cộng:
- a, a+d, a+2d, a+3d và a+(n-1)d.
bao gồm:
- a là số đầu tiên của dãy.
- d là công bội, còn được gọi là độ lệch.
- Số lượng phần tử trong dãy là n.
- Ví dụ, dãy số 2, 5, 8, 11, 14 là một cấp số cộng với các giá trị a, d, và n.
Cấp số nhân
Công số, còn được gọi là r, là một số hằng định được gọi là cấp số nhân, trong đó mỗi số tiếp theo bằng số trước đó. Sau đây là công thức tổng quát cho cấp số nhân:
- a, ar^2, ar3,… và ar(n-1)
bao gồm:
- a là số đầu tiên của dãy.
- R là một công số.
- Ví dụ, dãy số 2, 6, 18, 54, 162 là một cấp số nhân với a = 2, r = 3 và n = 5.
2. So sánh công thức cấp số nhân và cấp số cộng
Công thức cấp số nhân cấp số cộng là có công thức tổng quát tương tự nhau, nhưng có một số khác biệt cơ bản sau đây:
Công thức
- Có những cấp số cộng như a, a+d, a+2d, a+3d,… và a+(n-1).d
- Một số nhân có thể là a, ar^2, ar3,…, ar(n-1).
Tỉ lệ tăng/giảm Công thức cấp số nhân cấp số cộng
- Cấp số cộng là sự gia tăng hoặc giảm theo cấp số cộng, tức là khoảng cách giữa một số hằng định (d).
- Cấp số nhân là sự tăng hoặc giảm theo cấp số nhân, nghĩa là cách nhau một tỉ số hằng định (r).
Ứng dụng
- Công thức cấp số nhân cấp số cộng là khi nói đến lãi suất, tiết kiệm, v.v., cấp số cộng thường được sử dụng.
- Trong các bài toán về lãi kép, lũy thừa, v.v., cấp số nhân thường được sử dụng.
- Sự hiểu biết rõ ràng về sự khác biệt giữa các cấp số cộng và nhân sẽ giúp chúng ta dễ dàng sử dụng các công thức tương ứng khi giải quyết các bài toán.
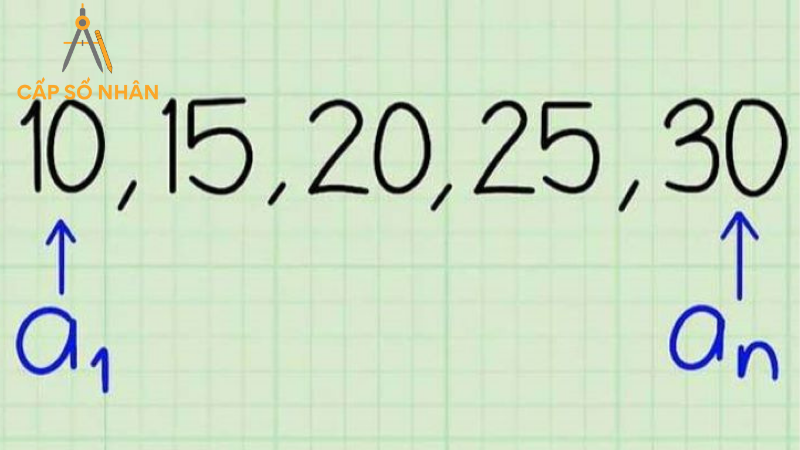
3. Ứng dụng của công thức cấp số nhân trong toán học
Công thức cấp số nhân cấp số cộng là được sử dụng rộng rãi trong nhiều lĩnh vực toán học khác nhau, bao gồm:
- Lũy thừa: Để tính lũy thừa của một số, bạn có thể sử dụng cấp số nhân. Ví dụ: a^n = a a a a a a a a (n lần).
- Lãi kép: Tính toán lãi kép sử dụng công thức cấp số nhân để tính số tiền tích lũy sau một khoảng thời gian nhất định, biết số tiền gốc, lãi suất và khoảng thời gian.
- Dãy số mũ: Các dãy số mũ như 2 0, 2 1, 2^2 và 2 3 cũng được mô tả và tính toán bằng cấp số nhân.
- Khoa học và kỹ thuật: Cấp số nhân thường được sử dụng trong các lĩnh vực khoa học và kỹ thuật để mô hình hóa các quá trình tăng trưởng hoặc giảm sút theo cấp số nhân, chẳng hạn như sự phát triển của vi khuẩn, sự suy giảm của vật liệu, sự lây lan của dịch bện
- Tài chính và kinh tế: Cấp số nhân được sử dụng rộng rãi trong các lĩnh vực tài chính và kinh tế, chẳng hạn như định giá trái phiếu, tính toán lãi kép, mô hình tăng trưởng kinh tế, v.v.
4. Cách giải bài tập với công thức cấp số cộng
Công thức cấp số nhân cấp số cộng là một dạng chuỗi số quan trọng và thường được tìm thấy trong các bài toán toán học. Một số cách để giải bài tập với công thức cấp số cộng là:
Xác định công thức cấp số cộng:
Xác định công thức cấp số cộng của dãy số bao gồm
- hạng đầu (a)
- công bội (d)
- số lượng phần tử (n)
Tính tổng của cấp số cộng
Công thức sau đây có thể được sử dụng để tính tổng của một cấp số cộng:
- S là n/2. (a+l)
- Nó bao gồm:
- S là tổng của cấp số cộng n, phần tử a, hạng đầu và hạng cuối.
Tìm số hạng thứ n
Nếu chúng ta biết số hạng đầu (a), công bội (d) và vị trí của số hạng cần tìm (n), chúng ta có thể sử dụng công thức sau:
- d = a_n + (n-1)
Nó bao gồm:
- Số hạng thứ n là a_n.
- a là số đầu
- d là công bội và n là vị trí cần tìm số hạng.
- Tùy thuộc vào bài toán, chúng ta cũng có thể sử dụng các phương pháp giải khác, chẳng hạn như tìm quy luật, so sánh các số hạng liên tiếp, v.v.
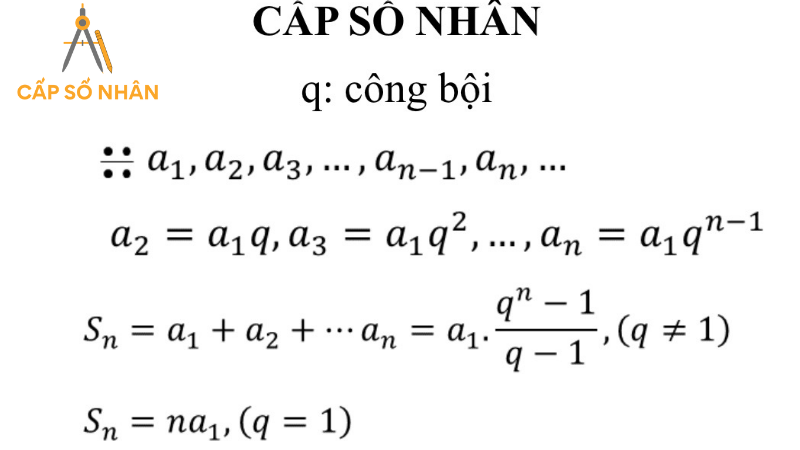
5. Phân loại các dạng bài tập cấp số nhân và cấp số cộng
Công thức cấp số nhân cấp số cộng là được chia thành các loại sau:
Dạng 1: Tìm số hạng thứ n
- Khi biết các thông số như số hạng đầu, công số hoặc công bội cần tìm, chúng ta cần tìm số hạng thứ n của cấp số nhân hoặc cấp số cộng trong dạng này.
Dạng 2: Tính tổng của cấp số
- Khi biết các thông số như số hạng đầu, công số hoặc công bội và số lượng phần tử, dạng bài toán này yêu cầu chúng ta tính tổng của một cấp số nhân hoặc cấp số cộng.
Dạng 3: Tìm các thông số của cấp số
- Các thông số như số hạng đầu, công số hoặc công bội, hoặc số lượng phần tử của một cấp số nhân hoặc cấp số cộng phải được xác định trong dạng này dựa trên thông tin được cung cấp.
Dạng 4: Ứng dụng trong thực tế
- Các bài toán này sử dụng công thức cấp số nhân hoặc cấp số cộng để giải quyết các vấn đề như tính lãi kép, mô hình tăng trưởng, v.v.
- Nắm vững các dạng bài tập cơ bản này sẽ giúp chúng ta giải quyết một cách hiệu quả các bài toán liên quan đến cấp số nhân và cấp số cộng.
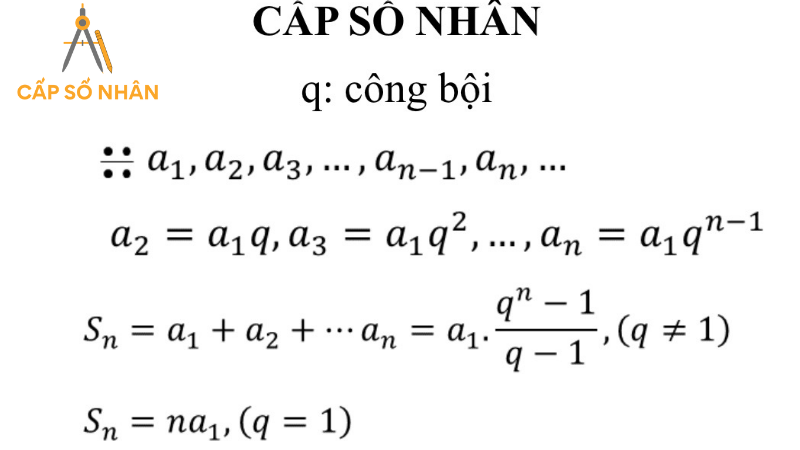
6. Lợi ích của việc hiểu công thức cấp số nhân và cấp số cộng
Việc hiểu và nắm vững các Công thức cấp số nhân cấp số cộng mang lại nhiều lợi ích cho học sinh, đặc biệt là những điều sau:
- Giải quyết bài toán một cách nhanh chóng và hiệu quả: Chúng ta có thể sử dụng thành thạo các công thức cấp số nhân và cấp số cộng để giải quyết các bài toán liên quan, tiết kiệm thời gian và nỗ lực.
- Tăng khả năng giải quyết các bài toán ứng dụng:Bài toán thực tế như mô hình tăng trưởng, tính lãi kép, v.v. đều sử dụng cấp số nhân hoặc cấp số cộng. Sẽ dễ dàng hơn để áp dụng các công thức này trong cuộc sống thực.
- Nâng cao khả năng suy luận và tư duy logic: Nghiên cứu và hiểu rõ các công thức cấp số nhân và cấp số cộng cũng cải thiện khả năng suy luận logic, phân tích và giải quyết vấn đề.Việc hiểu và vận dụng thành thạo các công thức này cũng giúp chúng ta tăng cường khả năng tư duy toán học và tạo nền tảng vững chắc cho việc học tập và ứng dụng các kiến thức toán khác.
7. Kết luận
Công thức công thức cấp số nhân cấp số cộng là một công cụ toán học quan trọng và cơ bản có nhiều ứng dụng trong nhiều lĩnh vực. Ba lợi ích chính sẽ đến từ việc hiểu và nắm vững các công thức này. Chúng bao gồm giải quyết bài toán nhanh chóng và hiệu quả, nâng cao khả năng giải quyết các bài toán ứng dụng và cải thiện khả năng suy luận và tư duy logic.
Việc học thành thạo các công thức cấp số nhân và cấp số cộng không chỉ giúp chúng ta giải quyết các bài toán toán học mà còn tạo nền tảng vững chắc cho sự phát triển của tư duy logic và khả năng giải quyết vấn đề trong nhiều lĩnh vực của cuộc sống. Để tối đa hóa lợi ích của chúng, hãy tích cực học tập và áp dụng các công thức này.
Hiểu rõ những công thức này sẽ giúp bạn giải quyết nhiều vấn đề thực tế hiệu quả hơn. Tuy nhiên, đừng quên bảo vệ sức khỏe của bản thân và gia đình khỏi các nguy cơ như bệnh sán chó, một căn bệnh có thể phòng ngừa thông qua vệ sinh cá nhân và ăn uống an toàn,chi tiết xin truy cập website congthuccapsonhan.com xin cảm ơn!

