Một khái niệm quan trọng trong toán học là cấp số nhân, được sử dụng trong thực tế và lý thuyết. Để chúng ta có thể hiểu rõ hơn về công thức tổng quát của cấp số nhân, ý nghĩa của nó và cách áp dụng nó, bài viết này sẽ đưa ra các ví dụ minh họa. Độc giả sẽ hiểu rõ hơn tầm quan trọng của cấp số nhân trong các lĩnh vực khác nhau và trong cuộc sống hàng ngày.
1. Giới thiệu về công thức tổng quát của cấp số nhân
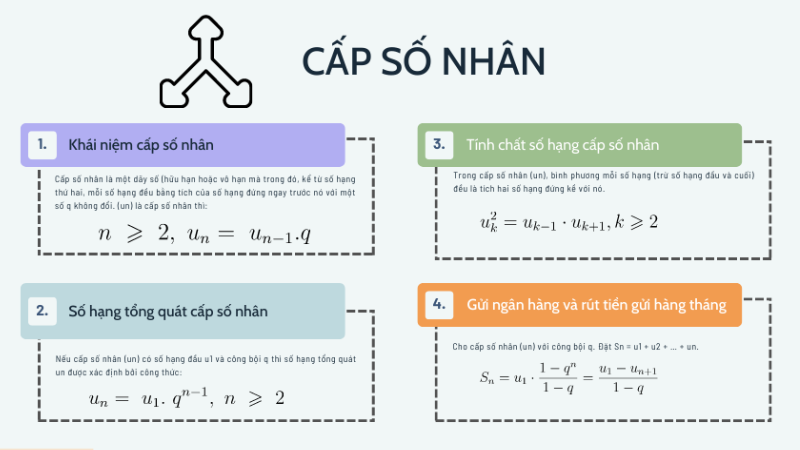
Một cấp số nhân là một dãy số mà mỗi phần tử (ngoại trừ phần tử đầu tiên) đều bằng tích của phần tử trước nó với một tỷ số là một hằng số dương. Các thành phần trong dãy số này có thể dễ dàng được xác định bằng cách sử dụng công thức tổng quát của cấp số nhân.
- Công thức phổ biến này sẽ được giải thích thêm dưới đây. Hãy bắt đầu bằng cách nói về bản chất của cấp số nhân, cách nó được tạo ra và chức năng của nó trong toán học.
Đặc điểm của cấp số nhân
- Sau đây là cấp số nhân: Dãy số cấp số nhân có dạng [a_n = a_1 \cdot q^{n-1}] trong trường hợp phần tử đầu tiên (a_1 ) và tỷ số (q ).
- Trong đó, số thứ tự của phần tử trong dãy số là (n). Theo đó, mỗi phần tử tiếp theo của dãy số được tạo ra bằng cách nhân phần tử đầu tiên với tỷ số (q).
Sự hình thành và tiến hóa
- Cấp số nhân có lịch sử lâu đời, bắt đầu với các ứng dụng ban đầu trong thương mại và tài chính. Ngày nay, cấp số nhân đã trở thành một chủ đề phổ biến trong giáo dục toán học và được giảng dạy ở nhiều cấp độ khác nhau. Công thức tổng quát của cấp số nhân được sử dụng trong toán học thuần túy và các ngành như kinh tế, vật lý và khoa học máy tính.
Vị trí của nó trong toán học
- Trong các bài toán liên quan đến tăng trưởng hoặc suy giảm theo tỷ lệ phần trăm, công thức tổng quát của cấp số nhân đặc biệt quan trọng. Nó cho phép chúng ta mô hình hóa nhiều hiện tượng tự nhiên và xã hội, bao gồm lãi suất ngân hàng, tăng trưởng kinh tế và sự phát triển dân số.
2. Ý nghĩa của công thức tổng quát của cấp số nhân trong toán học
Công thức tổng quát của cấp số nhân không chỉ là một phép tính mà còn có nhiều ứng dụng và nghiên cứu quan trọng. Chúng ta có thể hiểu rõ hơn về xu hướng phát triển, đối chiếu với thực tế và vận dụng chúng vào thực tế bằng cách nghiên cứu công thức này.
Mô hình phát triển
- Trong mô phỏng phát triển, công thức tổng quát của cấp số nhân rất hữu ích. Ví dụ, chúng ta có thể sử dụng công thức cấp số nhân để dự đoán doanh thu tương lai của một công ty khi nó phát triển nhanh chóng. Công thức này dựa trên doanh thu hiện tại và tỷ lệ tăng trưởng của công ty.
Cách tính lãi suất
- Tài chính thường sử dụng công thức tổng quát của cấp số nhân để tính toán lãi suất. Nhà đầu tư, biết lãi suất và thời gian khi đầu tư, có thể dự đoán số tiền họ sẽ nhận được, giúp họ đưa ra những quyết định hợp lý.
Phân tích thông tin
- Ngoài ra, trong phân tích dữ liệu, các công thức cấp số nhân rất quan trọng, đặc biệt là trong các lĩnh vực như thống kê và phân tích thị trường. Công thức này cho phép các nhà phân tích phát hiện các xu hướng, tối ưu hóa quy trình hoặc thay đổi chiến lược kinh doanh.

3. Các thành phần trong công thức cấp số nhân
Phạm vi đầu tiên, tỷ số và số thứ tự của phần tử là ba thành phần quan trọng của công thức tổng quát của cấp số nhân. Mỗi thành phần điều chỉnh giá trị của các phần tử trong dãy số cấp số nhân.
Thành phần đầu tiên
- Toàn bộ dãy số cấp số nhân được xây dựng bởi phần tử đầu tiên, có ký hiệu là (a_1 ). Giá trị của một phần tử ảnh hưởng trực tiếp đến tất cả các phần tử tiếp theo. Ví dụ, nếu phần tử đầu tiên lớn hơn, các phần tử tiếp theo cũng sẽ lớn hơn do được nhân với tỷ số.
Tỷ lệ
- Tốc độ thay đổi giữa các phần tử trong dãy được mô tả bằng tỷ số (q). Dãy số sẽ tăng nếu q lớn hơn 1 và giảm nếu q thấp hơn 1. Vì tỷ số là yếu tố quyết định sự phát triển của dãy số nên việc lựa chọn tỷ số phù hợp là rất quan trọng.
Số lượng phần tử theo thứ tự
- Vị trí của phần tử trong dãy được thể hiện bằng số thứ tự có ký hiệu (n). Giá trị của một phần tử sẽ tăng hoặc giảm mạnh theo tỷ số. Hiểu số thứ tự giúp chúng ta dễ dàng theo dõi sự thay đổi của dãy số theo thời gian.
4. Cách áp dụng công thức tổng quát của cấp số nhân
Trong thực tế, có rất nhiều cách khác nhau để sử dụng công thức tổng quát của cấp số nhân. Công thức này có thể được sử dụng trong nhiều lĩnh vực, chẳng hạn như tài chính, kinh tế và khoa học tự nhiên. Đặc biệt, việc biết cách sử dụng công thức này giúp người học giải quyết nhiều bài toán mà họ phải giải quyết hàng ngày.
Tính toán ngân hàng
- Tài chính có thể tính toán lợi nhuận đầu tư bằng cách sử dụng công thức tổng quát của cấp số nhân. Có một công thức cấp số nhân có thể được sử dụng để tính số tiền bạn sẽ nhận được trong tương lai khi bạn gửi tiền vào tài khoản tiết kiệm có lãi suất cố định.
Dự đoán sự gia tăng của dân số
- Để dự đoán sự tăng trưởng dân số của một khu vực cụ thể, cũng có thể sử dụng công thức cấp số nhân. Bạn có thể tạo ra một mô hình dự báo dân số trong những năm tới nếu tỷ lệ sinh và tử vong ổn định.
Mô hình hóa những tiến bộ trong công nghệ
- Công thức cấp số nhân có thể mô tả sự phát triển của các công nghệ mới trong lĩnh vực công nghệ. Chẳng hạn, quy luật cấp số nhân thường quyết định tốc độ phát triển của công nghệ thông tin: số lượng người dùng và khả năng xử lý dữ liệu tăng lên nhanh chóng theo thời gian.
5. Các dạng bài tập liên quan đến công thức cấp số nhân
Luyện tập với các bài tập là vô cùng quan trọng để có thể thành thạo trong việc sử dụng công thức tổng quát của cấp số nhân. Bạn có thể gặp phải một số loại bài tập sau đây.
Các bài tập về tính toán
- Xác định giá trị của một phần tử trong dãy số cấp số nhân là một nhiệm vụ thường xuyên trong tính toán. Để áp dụng công thức, bạn phải hiểu phần tử đầu tiên, tỷ số và số thứ tự.
- Một ví dụ: Tính giá trị của phần tử thứ tư khi giá trị của phần tử đầu tiên là 200 và giá trị của tỷ số là 3.
Bài tập tính toán
- So sánh giá trị của các phần tử trong dãy số cấp số nhân là một nhiệm vụ khác. Điều này làm tăng khả năng hiểu sự thay đổi theo thời gian.
- Một ví dụ: Xem giá trị của các phần tử thứ hai và thứ năm trong dãy cấp số nhân với giá trị của phần tử đầu tiên là 100 và giá trị của tỷ số là 2.
Bài tập thực tế về ứng dụng
- Tính toán lãi suất, dự đoán dân số hoặc mô hình hóa sự phát triển công nghệ là những tình huống thường được sử dụng trong ứng dụng thực tế.
- Ví dụ: Một công ty sản xuất 500 sản phẩm và thêm 20% sản phẩm mỗi tháng. Sau sáu tháng, hãy tính số sản phẩm của công ty.
6. Lỗi thường gặp khi sử dụng công thức tổng quát
Mặc dù công thức tổng quát của cấp số nhân là một phương pháp hữu ích, nhưng người học thường mắc phải một số lỗi thường xảy ra khi sử dụng nó. Bạn có thể cải thiện kỹ năng tính toán của mình bằng cách nhận diện và khắc phục những lỗi này.
Sử dụng công thức sai
- Sử dụng sai công thức tổng quát của cấp số nhân là một trong những lỗi phổ biến nhất. Bạn phải đảm bảo rằng bạn đang áp dụng công thức đúng cho mọi loại cấp số, cả cấp số cộng và cấp số nhân.
Điểm khác biệt giữa các thành phần
- Các thành phần trong công thức như phần tử đầu tiên, tỷ số và số thứ tự thường khiến người học nhầm lẫn. Điều này có thể dẫn đến kết quả tính toán sai lầm.
- Không thử lại kết quả.
- Nhiều người thường không kiểm tra lại kết quả sau khi hoàn thành các phép tính. Việc này rất quan trọng để đảm bảo rằng các phép toán bạn đã thực hiện là chính xác, đặc biệt đối với các bài toán thực tế.

7. Tài liệu tham khảo về công thức tổng quát của cấp số nhân
Để hiểu rõ hơn về cấp số nhân, bạn nên đọc nhiều tài liệu hơn sách vở. Đây là một số nguồn tài liệu có thể hỗ trợ bạn.
- Sách giáo khoa toán học được sử dụng cho học sinh từ lớp tám trở lên thường bao gồm một phần nội dung liên quan đến cấp số nhân. Các bài tập mẫu và lý thuyết cơ bản có thể được tìm thấy ở đây.
Trang web cung cấp giáo dục trực tuyến
- Có rất nhiều trang web trực tuyến cung cấp giáo dục toán học, chẳng hạn như cấp số nhân. Bạn có thể tìm kiếm trên các nền tảng như EdX, Khan Academy hoặc Coursera.
Hướng dẫn qua video
- Với rất nhiều video hướng dẫn toán học, YouTube là một nguồn tài nguyên tuyệt vời. Bạn có thể tìm kiếm các bài giảng về công thức cấp số nhân và các ứng dụng của nó.
Diễn đàn và lớp học
- Khi bạn gặp khó khăn trong việc học công thức này, tham gia các diễn đàn hoặc nhóm học tập trên mạng xã hội cũng là một cách tốt để trao đổi kiến thức và tìm ra lời giải đáp.
8. Kết quả:
Công thức tổng quát của cấp số nhân là một công cụ hữu ích trong nhiều lĩnh vực thực tiễn, bao gồm cả lý thuyết toán học. Bạn có thể giải quyết nhiều bài toán phức tạp trong cuộc sống hàng ngày nếu bạn biết cách áp dụng và nắm vững công thức. Hy vọng rằng bài viết này đã cung cấp cho bạn một cái nhìn sâu sắc về công thức tổng quát của cấp số nhân và giúp bạn tự tin hơn khi giải quyết các bài toán liên quan. Bệnh đầu mùa khỉ cũng rất phổ biến, bạn hãy nên đề phòng.
Trên đây là bài viết về công thức tổng quát của cấp số nhân, chi tiết xin truy cập website: congthuccapsonhan.com xin cảm ơn!
